Referenzfrequenz "reinigen"
Mittenfrequenz
Bandbreite
Bauteileauswahl
nötige Formeln
Fazit
| Allgemeines Referenzfrequenz "reinigen" Mittenfrequenz Bandbreite Bauteileauswahl nötige Formeln Fazit |
|
| Die externe Referenzfrequenz für Messgeräte
sollte ein sauberer 10-MHz Sinus sein, der an einer 50-Ohm
Last einen Pegel von etwa 0,5 Vrms bis 2 Vrms haben sollte.
Professionelle Referenzfrequenzquellen liefern dass
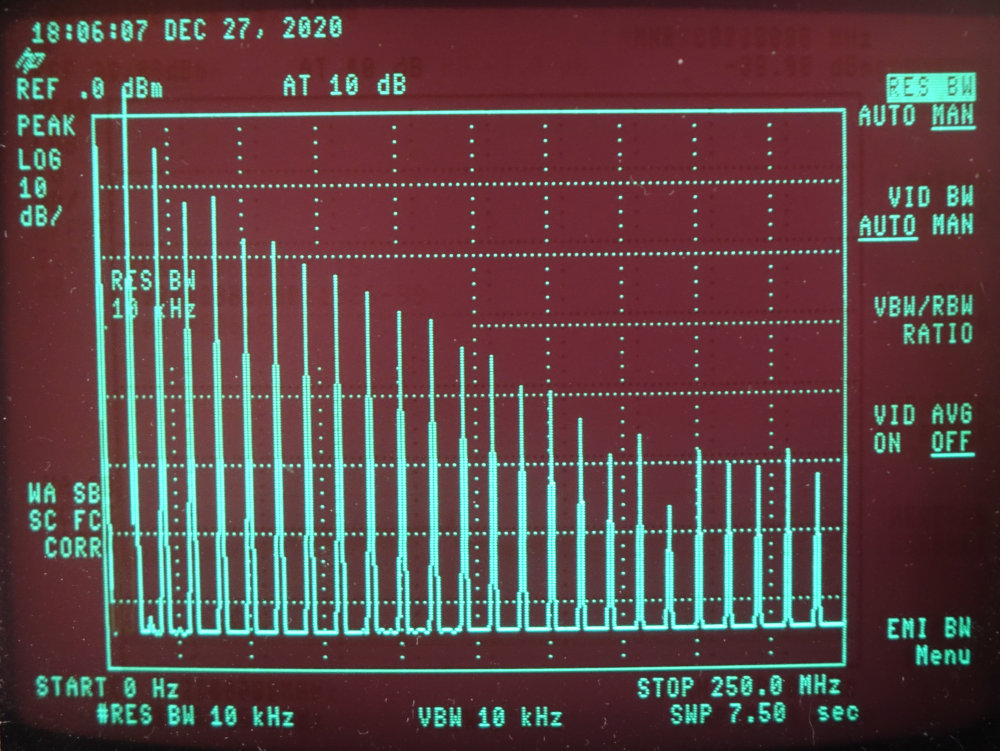
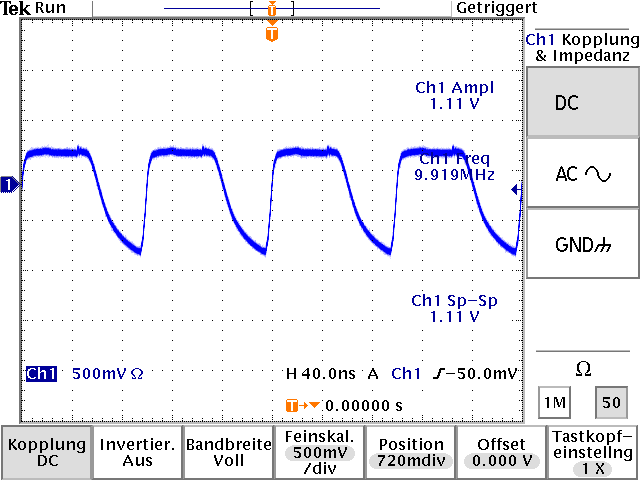
natürlich auch. Baut man sich seine Referenzfrequenzquelle selber, startet man oft mit einem 10MHz-Signal, das in irgendeiner hässlichen Form aus einem OCXO, TCXO oder Rubidium-Element kommt. Nebenstehend haben wir das Ausgangssignal eines preiswerten OCXO-Modules (chinesischer Ebay-Händler) an einer 50 Ohm Last. Rechts ist das Oszillogramm, und links das Spektrum im Bereich bis 250 MHz. Die 10 MHz-Linie ist im Spektrum zwar die Größte, aber es gibt alle 10 MHz Oberwellen. Die müssen weg. Das geht recht einfach mit einem 10 MHz Bandpassfilter. |
 |
 |
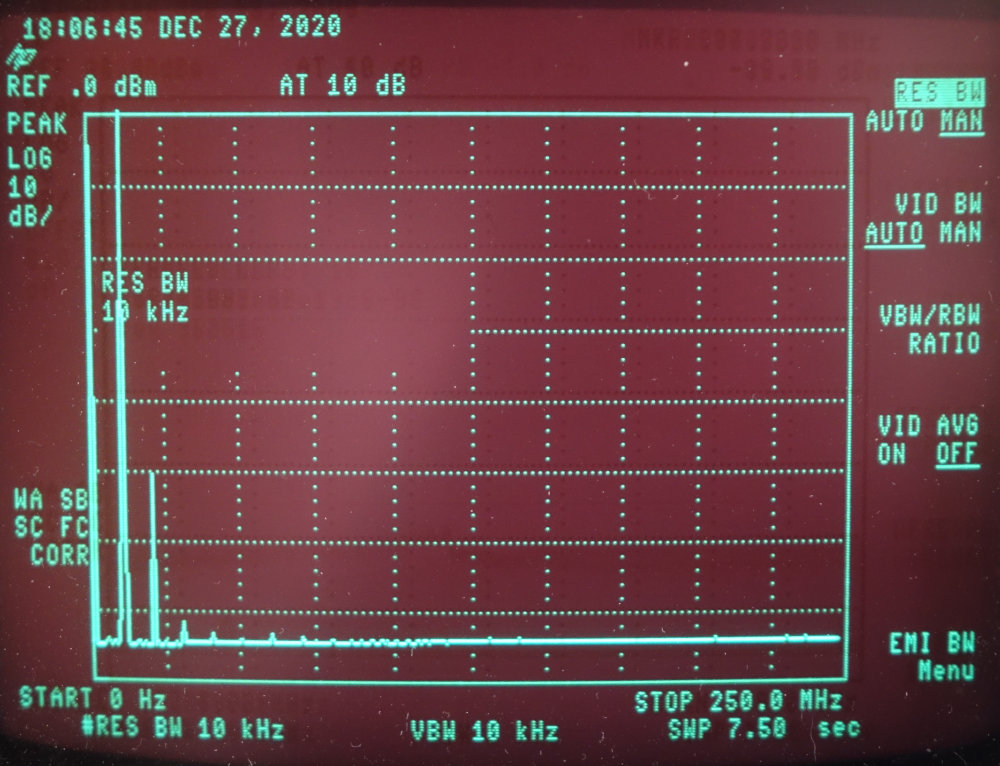
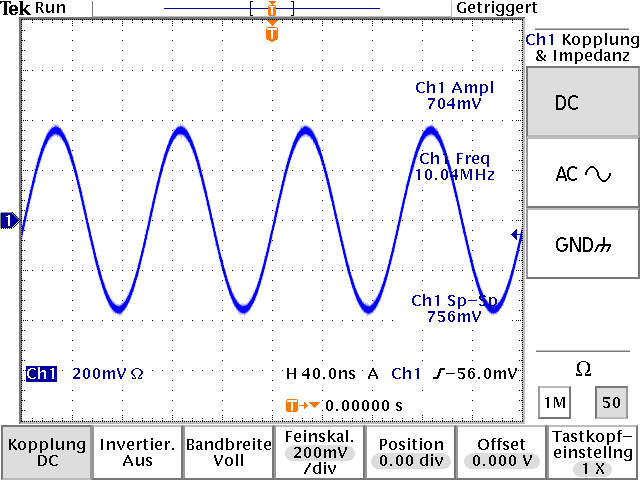
| Ein gerade einmal aus vier passiven Bauteilen
bestehender Filter räumt das Signal auf. Nebenstehend sehen
wir das Ergebnis. Neben der 10-MHz-Linie ist gerade noch die
20 MHz-Linie zu erkennen, aber diese ist schon 50 dB kleiner
(1/100000). Das Ergebnis ist ein sauberer 10 MHz-Sinus. Das
dieser etwas kleiner ist als das Original, lässt sich nicht
vermeiden. Verluste gibt es in der realen Welt immer, und
schließlich wurde ja durch das Filter auch Energie
"weggefiltert". Ich nutze diese Gelegenheit, um einmal die Grundlagen eines Bandpassfilters zu erläutern. Das Beispiel ist relativ einfach. Zum einen ist 10 MHz noch keine sehr hohe Frequenz, und deshalb gut beherrschbar. Zum anderen brauchen wir keinen sehr guten Filter. Er muss weder sehr genau noch sehr schmalbandig sein. Die Mittelfrequenz des Filters sollte etwa bei 10 MHz liegen. Da die nächste zu unterdrückende Frequenz erst 20 MHz ist, darf der Filter aber recht breitbandig sein. Bei einer Bandbreite von 1 ... 2 MHz ist es dann auch gar nicht schlimm, wenn die Mittenfrequenz um z.B. 200 kHz zu hoch oder zu niedrig ist. Das 10 MHz-Signal liegt dann immer noch sicher im Durchlass-Band. Ach ja: Bandbreite. Das ist der Frequenzbereich, in dem - von der Mittelfrequenz aus gesehen - das Signal um nicht mehr als 3dB abgeschwächt wird. Da 3dB aber nur 50% sind, sollte das nächste störende Signal also nicht an diese Bandgrenze liegen, dann wäre es ja nur auf die Hälfte abgeschwächt. Deshalb zielte ich eine Bandbreite von 1 ... 2 MHz an, obwohl die nächste störende Frequenz 10 MHz weit weg ist. Das garantiert eine ausreichende Dämpfung. |
 |
 |
| Dafür reicht wirklich schon die billigste und
einfachste Schaltung aus. Hier sehen wir sie: Kernelement sind C2 und L2. Diese bilden einen Reihenresonanzkreis mit einer Frequenz von etwa 10 MHz. (In Wirklichkeit sind es 9,7 MHz, da ich auf handelsübliche Bauteile zurückgegriffen habe.) So ein Reihenresonanzkreis hat bei seiner Resonanzfrequenz den Widerstand Null. Er lässt 10 MHz also einfach durch, das ist schon mal gut. Genaugenommen haben C2 und L2 bei 10 MHz imaginäre Widerstände mit gleicher Größe (600 Ohm) und entgegengesetzten Vorzeichen. Durch die Reihenschaltung addieren diese sich auf und ergeben -600+600=0. Ist hinter dem Filter ein Verbraucher mit 50 Ohm Eingangsimpedanz angeschlossen, dann hat nun das Filter automatisch diese Impedanz als Eingangsimpedanz, da es selber bei 10 MHz ja keinen zusätzlichen Widerstand hat. Bei größeren oder kleineren Frequenzen als 10 MHz wird der Widerstand zwar größer als Null, dass würde aber nur zu einer recht kleinen Dämpfung dieser Frequenzen führen. Nun kommen C1 und L1 ins Spiel, die einen 10-MHz-Parallelresonanzkreis bilden. |
 |
 |
| L1 ist eine kleine Luftspule, die nur aus 6
Windungen besteht, die über ein 4mm-Rohr gewickelt wurden.
Die ist also eigentlich nur ein Stück Draht. Für niedrige
Frequenzen stellt sie einen Kurzschluss dar. Für niedrige Frequenzen ist deshalb die Eingangsimpedanz des Filter nahezu 0 Ohm, und das eingehende niederfrequente Signal wird wegen dieser Impedanzfehlanpassung zurück reflektiert. Mit steigender Frequenz steigt auch die Impedanz der Spule, und es wird immer weniger der reinkommenden Energie reflektiert. Im nebenstehenden Durchlassdiagramm des Filters ist L1 also für den ansteigenden Ast von der linken unteren Ecke bis zum "Gipfel" verantwortlich. C1 ist ein vergleichsweise großer Kondensator (verglichen mit C2). Für hohe Frequenzen (>>10MHz) stellt er einen Kurzschluss dar. Für hohe Frequenzen ist deshalb die Eingangsimpedanz des Filter nahezu 0 Ohm, und das eingehende hochfrequente Signal wird wegen dieser Impedanzfehlanpassung zurück reflektiert. Mit sinkender Frequenz steigt auch die Impedanz des Kondensators und es wird immer weniger der reinkommenden Energie reflektiert. Im nebenstehenden Durchlassdiagramm des Filters ist C1 also für den Ast rechts vom "Gipfel" verantwortlich. Bei etwa 10 MHz haben C1 und L1 jeweils 4 Ohm Impedanz, aber mit unterschiedlichen Vorzeichen. In der Parallelschaltung führt das zusammen zu einem unendlich hohen Widerstand. Bei 10MHz kann man also so tun, als ob C1 und L1 gar nicht existieren. |
 |
 |