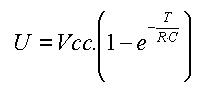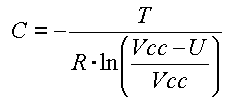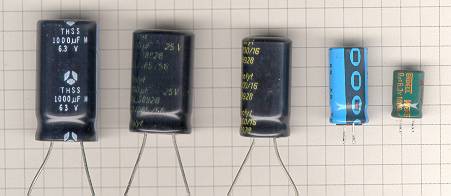Messungen an Induktivitäten und Kondensatoren

Messung der Spulenparameter

• Innenwiderstand
• Induktivität
• Kernverluste
• Sättigungsstrom

Bestimmung des Spuleninnenwiderstandes

Der Innenwiderstand lässt sich am einfachsten bestimmen.

Eine direkte Messung ist aber nicht ganz einfach. Die Widerstandsmessfunktion eines Multimeters eignet sich für so kleine Widerstände gar nicht. Wer ein regelbares Netzteil mit einstellbarere Strombegrenzung sein Eigen nennt, kommt aber auch zum Ziel.
 

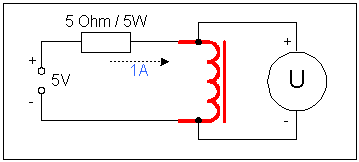
Das Netzteil wird an die Spule angeschlossen, und ein Strom von 1 A eingestellt. Mit einem Digitalvoltmeter wird nun die Spannung über der Spule gemessen. Dabei ist es wichtig, das Multimeter direkt am Spulendraht anzuschließen, und nicht etwa am Netzteil oder an den Anschlussleitungen!! Die gemessene Spannung in Millivolt entspricht dem Spulenwiderstand in Milliohm. Wer ein regelbares Netzteil ohne Strombegrenzung hat, kann einen 5-Ohm-Widerstand (5 Watt !) mit der Spule in Reihe schalten (siehe Abbildung), und diese Kombination an das Netzteil anschließen. Sodann ist das Netzteil auf 5V einzustellen. Schon hat man den geforderten Strom von 1A.

Beispiel:
Eine Spule wird in die obrige Schaltung eingesetzt, und mit 1A (DC) gespeist. Das parallel angeschlossene Voltmeter misst über der Spule eine Spannung von 18mV (DC). Der Spuleninnenwiderstand beträgt folglich 18 Milliohm.
 

Besteht eine Spule aus mehreren parallelen Wicklungen, so sollte man für die Messung die einzelnen Drähte sicher durch verlöten verbinden, und nicht etwa mit einer Krokoklemme zusammenklemmen.

Der Innenwiderstand lässt sich auch ausrechnen. Dazu benötigt man:

• die Anzahl der Windungen
• den Drahtquerschnitt
• die Länge einer einzelnen Windung

• A = 0,785 * d²

• R = 0,178 * L / A  = 0,227 * L / d²   [in Milliohm]

Bestimmung der Spuleninduktivität

Wenn man kein Induktivitätsmessgerät besitzt, lässt sich die Induktivität am einfachsten nach der Resonanzmethode bestimen. Dafür benötigt man einen abstimmbaren Sinusgenerator (1..100 kHz), einen möglichst großen ungepolten Kondensator, einen einfachen 100 nF Kondensator und ein Multimeter, mit dem man Wechselspannungen und Frequenzen messen kann. Der Sinusgenerator sollte am Ausgang nicht zu hochohmig sein. Ein 50-Ohm-Ausgang ist geeignet.
 

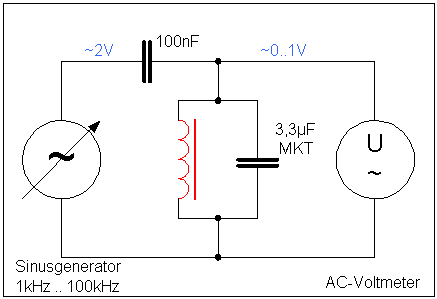Man baut aus der unbekannten Spule und dem großen ungepolten Kondensator (ich benutze immer einen 3,3µF-MKT-Kondensator, besser wäre wohl ein 1µF-Keramik-Vielschichtkondensator) einen Schwingkreis auf. Über den 100-nF-Kondensator speist man das Signal des Sinusgenerators ein. Mit dem Voltmeter misst man die Amplitude der Schwingung im Schwingkreis. Durch langsames Durchstimmen des Generators sucht man die Frequenz, bei der die Schwingamplitude maximal ist. Das ist die Resonanzfrequenz des Schwingkreises. Nun misst man diese Frequenz mit dem Multimeter. Die Induktivität errechnet man nach: L = 1 / (39,5 * C * f2) wobei C der Schwingkreis-Kondensator (hier also 3,3µF = 0,0000033 F) ist.

ACHTUNG:
Viele Multimeter können Wechselspannungen nur im Bereich 40Hz bis 1 kHz korrekt messen, danach steigt zunächst der Messfehler (was hier nicht so wichtig ist). Oberhalb einer Frequenz von einigen 10kHz versagen sie dann total. Deshalb sollte bei der Dimensionierung des Schwingkreis-Kondensators oder der Wahl des Messgerätes darauf geachtet werden, dass das Messgerät die entstehende Wechselspannung noch messen kann.
Als ideales Alternativmessgerät bietet sich natürlich der Oszi an.

Messgenauigkeit
Die Güte des Resonanzkreises ist erfahrungsgemäß hoch genug, um den Resonanzpunkt präzise einzustellen. Begrenzt wird die Einstellgenauigkeit nur von den Bedienelementen des Sinusgenerators. (Wenn mit einer einzigen Poti-Drehung von 10Hz bis 1MHz durchgestimmt wird, dann ist die Einstellgenauigkeit naturgemäß begrenzt.)
Wenn das Multimeter die Frequenz nach dem Zählfrequenz-Messverfahren bestimmt, sind hier keine nennenswerten Messfehler zu erwarten. Ein Eigenbau-Frequenzzähler mit geeignetem Vorverstärker kann ebenso genutzt werden.
Die Toleranz des Schwingkreis-Kondensators wirkt sich direkt auf die Messgenauigkeit aus. Ein 10% zu großer oder zu kleiner Kapazitätswert führt zu einer 10% zu klein oder zu groß bestimmten Induktivität.

Beispiel:
In obriger Schaltung wird z.B. in weiten Frequenzbereichen eine extrem kleine Spannung am Voltmeter gemessen. Doch etwas unter 10 kHz steigt die Spannung auf einige 100mV. Das Maximum wird mit 320 mV (AC) festgestellt. Nach Umschaltung in den Frequenzmessbereich zeigt das Multimeter eine Frequenz von 8,95 kHz. Daraus errechnet man eine Induktivität von 95 µH für die Spule.

Für den 3,3-µF-Kondensator bzw. einen 1-µF-Kondensator ergeben sich etwa folgende Frequenzen:
 

Induktivität	Frequenz für 3,3µF	Frequenz für 1µF
1 µH	90 kHz	160 kHz
10 µH	27 kHz	50 kHz
100 µH	9 kHz	16 kHz
1 mH	2,7 kHz	5 kHz

Die so ermittelte Induktivität gilt nur für kleine Spulenströme. Bei großen Strömen bricht die Induktivität auf 50% zusammen.

Ist die Induktivität L ermittelt, dann läss sich der AL-Wert des Spulenkerns aus der Induktivität L und der Windungszahl N berechnen:

• AL = L / N²

• Es sollte unbedingt ein Sinusgenerator verwendet werden. Beim Einsatz eines Rechteckgenerators, erregen auch dessen Oberwellen den Schwingkreis, so dass es zu einer mehrdeutigen Messung kommt. Der Schwingkreis lässt sich dann durch verschiedene Frequenzen erregen.
• Als Schwingkreis-Kondensator sollte kein ELKO verwendet werden, da diese bei hohen Kapazitäten gänzlich andere Kapazitäten zu haben vorgeben. Ein 1000µF-Elko kann sich bei 500kHz wie ein 1nF-Kondensator verhalten, da dann der innere Wickel durch seine Induktivität praktisch von der Schaltung isoliert ist, und nur noch das Gehäuse die Induktivität bestimmt - in diesem Fall 1nF.

Bestimmung der Kernsättigung / Induktivitätsabnahme bei Gleichstrombelastung - Variante 1

Die Spuleninduktivität sinkt mit dem Strom durch die Spule, und erreicht ihr Minimum, wenn der Kern gesättigt ist.
 

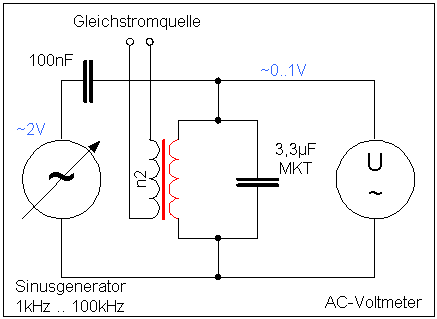In nebenstehender Schaltung wird der Kern der Spule mit Hilfe einer zweiten Wicklung vormagnetisiert. Dafür wird diese zweite Wicklung (mit der Windungszahl n2) von einem Gleichstrom durchflossen. Für jeden Gleichstrom kann nun wie oben (nach der Resonanzmethode) die Induktivität bestimmt werden. Die gemessene Induktivität gilt dann für das Produkt aus dem Gleichstrom und der Windungszahl n2. Die Spule hat also bei doppeltem Strom und halber Windungszahl die gleiche Induktivität. Beispiel:  Es soll ermittelt werden, welche Induktivität eine Spule mit 20 Windungen bei 10A hat. Da 10A nicht zur Verfügung stehen, wickelt man 100 Windungen als zweite Wicklung auf den Kern, und speist in diese Wicklung 2A (2A * 100Wdg. = 10A * 20Wdg.). Die gemessene Induktivität gilt dann auch für 10A bei 20 Windungen. Auf diese Art und Weise lässt sich die Induktivitätsabnahme der Spule, und damit auch die Sättigung bestimmen.

ACHTUNG:
Schon das Aufwickeln der zweiten Spule verändert die Resonanzfrequenz des Schwingkreises (durch die kapazitive Wirkung der übereinandergewickelten Spulen). Die Frequenz muss also neu bestimmt werden.
Die über die Gleichstromquelle quasi kurzgeschlossene zweite Spule stellt für den Schwingkreis eine starke Belastung dar, die zu einer starken Bedämpfung führt. Hochinduktive Spulen (die aber gleichzeitig große Ströme Vertragen müssen) in den Zuleitungen zur zweiten Spule könnten das Problem vermindern.
Das Messverfahren ist also alles andere als ideal, aber es benötigt wenigstens keine teure Messtechnik.

Beispiel:
Es soll überprüft werden, bis zu welchem Strom eine 100-µH-Spule benutzt werden kann, wobei ihre Induktivität nicht unter 50 µH fallen darf:
Die Schaltung wird aufgebaut, die zweite (im Bild linke) Spule ist noch stromlos. Es wird die Induktivität bestimmt, wobei eine Frequenz von ca. 9 kHz als Schwingfrequenz ermittelt wird. Damit steht die Grundinduktivität mit 100 µH fest.
Man ermittelt nun die Schwingfrequenz des Schwingkreises für eine Induktivität von 50 µH. Nach der allgemeinen Schwingkreisformel sind das 12,4 kHz:

• f = 1 / (6,28 * Wurzel( C * L)) = 1 / (6,28 * Wurzel (3,3µF * 50µH)) = 12,39kHz

Bestimmung der Kernsättigung / Induktivitätsabnahme bei Gleichstrombelastung - Variante 2

Bei steigendem Strom durch die Spule sinkt ihre Induktivität. Die Spuleninduktivität sinkt mit dem Strom durch die Spule, und erreicht ihr Minimum, wenn der Kern gesättigt ist. Da Spulen in Schaltreglern meist von großen Gleichströmen durchflossen werden, ist es wichtig zu wissen, bis zu welchem Strom die Spule belastet werden kann, ohne dass der Kern in Sättigung gerät, und die Spule sich nur noch wie eine Luftspule verhält.

Wird an eine Spule eine konstante Spannung angelegt, so setzt ein Stromfluss ein, der bei Null beginnend gleichmäßig ansteigt. Die Steigung hängt von der Induktivität der Spule ab: je höher die Induktivität, desto langsamer der Stromanstieg. Da mit steigendem Spulenstrom die Induktivität abnimmt, steigt der Spulenstrom mit der Zeit immer schneller. Das lässt sich mit einem Oszi (am Besten einem Speicheroszi) auswerten.

Benötigt wird ein Netzteil und ein Messwiderstand. Das Netzteil muss eine Spannungsstabilisierung und eine Strombegrenzung haben. Die Spannungsstabilisierung sorgt für eine gleichmäßige Speisung der Spule, auch wenn der Strom schnell ansteigt. Die Strombegrenzung ist nötig, da der steigende Spulenstrom das Netzteil nach wenigen Millisekunden kurzschließt.
Das Netzteil muss in der Lage sein, sehr schnell auf Laständerungen zu reagieren. Es sollte in 100 µs eine Stromänderung von 2 A vertragen. Ein 'Conrad PS-302A' erwies sich als untauglich, da es die Ausgangsstromänderung auf 60mA/ms begrenzte (viel träger als die zu messenden Spulen). Ein altes 'Statron 3205' aus DDR-Produktion erfüllte dagegen die Anforderungen klaglos.
Der Messwiderstand muss so klein sein, dass sein Spannungsabfall die Messung nicht wesentlich verfälscht. Ich benutze einen 0,033 Ohm Widerstand. Werte bis zu 0,27 Ohm wären akzeptabel.
 

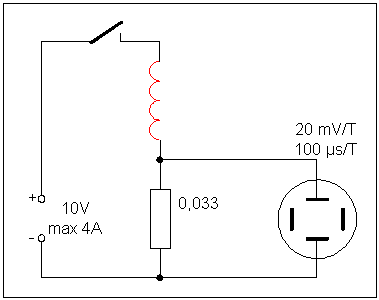Am Speicheroszi wird der Anstieg des Spannungsabfalls  über dem Messwiderstand nach Einschalten des Stromes gemessen. Bei einem 2-Kanal-Speicheroszi lässt sich im zweiten Kanal dabei die 10V-Spannung beobachten (um ein eventuelles Einbrechen der Spannung durch die Last zu erkennen).

Beispiel
Der Kern einer 10-A-Siebdrossel wurde mit 127 Windungen versehen und ausgemessen.
Die Spannung am Messwiderstand steigt in den ersten 360 µs von 0 V auf 70 mV. In den folgenden 200 µs steigt sie um weitere 55 mV auf nun 125 mV. Auf dem zweiten Oszi-Kanal konnte gleichzeitig beobachtet werden, die die Netzteilspannung im ersten Abschnitt bei ca. 10,3 V lag, und im zweiten Abschnitt auf durchschnittlich 9,4 V zusammenbrach.
Trotz kleinerer Netzteilspannung war der Spannungsanstieg im zweiten Abschnitt steiler, was auf die Induktivitätsabnahme zurückzuführen ist.
 

	1. Abschnitt	2. Abschnitt
Netzteilspannung U	10,3 V	9,4 V
Spannung am Anfang Ua	0V	70 mV
Spannung am Ende Ue	70 mV	125 mV
Spannungsanstiegt dU = Ue - Ua	70 mV	55 mV
Stromanstieg dI = dU / 0,033 Ohm	2,12 A	1,66 A
Zeitdauer dt	360  µs	200 µs
Induktivität L = U * dt / dI	1,75 mH	1,12 mH
AL-Wert	103 nH	66 nH

Aus diesen Werten lassen sich Wickeldaten ermitteln. Aus obriger Tabelle kann man entnehmen, dass der AL-Wert mit dem Produkt aus Windungszahl und Strom (bei mir Kerbelastung genannt) abnimmt. Folglich benötigt eine 40 µH-Spule bei höherem Strom auch mehr Windungen.

In der unteren Tabelle sind zwei Varianten einer 40-µH-Spule mit diesem Kern ausgerechnet worden. Bei einem Strom von 7 A werden 19 Windungen benötigt. Bei einem Strom von 15 A dagegen 25 Windungen, um den schwindenden AL-Wert zu kompensieren. Die Kerbelastungen der beiden Beispielspulen entsprechen den Belastungen während der Messung in den Abschnitten 1 und 2.
 

	1. Abschnitt	2. Abschnitt
Windungszahl N bei der Messung	127	127
durchschnittlicher Strom	1,06 A	2,95 A
durchschnittliche Kernbelastung Bel = I * N	135 A	374 A
Windungszahl für 40 µH n = Wurzel(L / AL)	19 Wdg.	25 Wdg.
Maximaler Strom bei 40 µH i = Bel / N	7 A	15 A

ACHTUNG:
Die Induktivität lässt sich nach diesem Verfahren nicht für einen Punkt, sondern nur durchschnittlich für einen Bereich bestimmen.

Die Kapazität (C) eines ELKOS bestimmt man am besten über sein Aufladeverhalten. Man speist in einen leeren ELKO einen Strom (I) ein, und stellt fest, auf welche Spannung (U) er sich innerhalb einer bestimmten Zeit (T) aufgeladen hat. Wenn man mit einem konstanten Strom lädt ist das recht einfach, da dann die Spannung mit der Zeit linear ansteigt.  Es gilt:

Man lädt den Elko mit einem konstanten Strom bis aus eine bestimmte Spannung auf, und misst die dafür nötige Zeit. Anschließend kann man die Kapazität berechnen. Leider benötigt man dafür eine Konstantstromquelle.

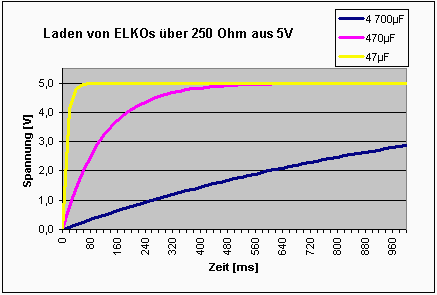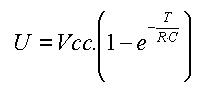
Man kann den ELKO auch einfach aus einer konstanten Spannung (Vcc) über einen Widerstand (R) laden. Dabei verringert sich aber im Laufe der Ladeprozedur der Ladestrom. Die Kondensatorspannung (U) steigt nicht linear an, sondern nach der Formel: Stellt man die Formel nach der Kapazität um, erhält man:

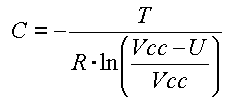
Nun sind vielen Leuten Logaritmen nicht gerade sympatisch, wenn man die Messung aber so durchführt, dass der Elko bis auf eine festgelegte Spannung aufgeladen wird, und man dabei die Zeit stoppt, dann ist der Logaritmus ein fester Wert, der für jede Messung identisch ist. Für Vcc=5V und U=2,5V ergibt der Logaritmus  -0,7.  Damit vereinfacht sich die Formel auf:

Das gilt immer, wenn man den ELKO über den Widerstand R aus einer 5V-Spannungsquelle von 0V auf 2,5V auflädt. Die Kapazität ist also der Ladezeit proportional.

Beispiel:
Vcc = 5 V;  U = 2,5 V;  R = 250 Ohm;  T = 0,814 s

C = 1,44 x T / R
C = 1,44 x 0,814 / 250
C = 0,0047 F = 4700 µF

Zur Durchführung der Messung eignet sich ein Speicher-Oszilloskop oder ein spezielles selbstgebautes Messgerät.

Was ist den der ESR überhaupt?
Das ist der Innenwiderstand des Kondensators, durch den der Strom in den Kondensator hinein und auch wieder hinaus muss. Es ist also prinzipiell ein scheinbarer Widerstand, der mit der Kapazität in Reihe geschaltet ist. Dieser interne Widerstand ist bauartbedingt, und ensteht durch den Widerstand der Anschlüsse und der Folienwickel im Kondensator. Einige 10 Milliohm sind typisch für einen ELKO.

Warum ist ein kleiner ESR wichtig?
Der Elko puffert die Energie am Schaltreglerausgang. Diese Energie fließt zweimal durch den Elko-ESR: einmal hinein in den ELKO und einmal wieder hinaus. Der ESR verursacht dabei Verluste und ein Schwanken der Ausgangsspannung. Ein 10A-Step-Down-Wandler mit einem DutyCycle von 0,5 lädt den ELKO mit 10A und entlädt ihn (über den Ausgang) wieder mit 10A. Bei einem ESR von 50 Milliohm bewirken 10A einen Spannungsabfall von 0,5 Volt. Beim Laden des Ausgangs-ELKOs liegt die Ausgangsspannung deshalb 0,5V höher als die ELKO-Spannung, beim Entladen aber 0,5V tiefer. Auch ein unendlich großer ELKO schafft es also nicht, die Ausgangsspannung stabil zu halten. Die 50 Milliohm ESR führen unabhängig von der ELKO-Kapazität zu einer Spannungsschwankung von 1 V am Reglerausgang!!

Impedanz des Kondensators
Jeder Kondensator hat einen Wechselstromwiderstand (die Impedanz), die normalerweise für das Filtern verantwortlich ist. Das heißt, der Kondensator wirkt für Wechselstrom wie ein Widerstand. Der Wechselstromwiderstand des Kondensators sinkt mit der Frequenz. Hohe Frequenzen werden vom Kondensator quasi kurzgeschlossen. Damit filtert der Elko die Schaltfrequenz aus dem Schaltreglerausgang.
Man ermittelt den Wechselstromwiderstand wie folgt:

• Z = 1/ (6,28 * f * C)

Daraus erkennt man, das bei großen Kondensatoren und hohen Frequenzen der ESR des Kondensators größer ist, als sein Wechselstromwiderstand. Da in einem Elko ESR und Impedanz in Reihe geschaltet sind, kann der Gesamtwechselstromwiderstand des ELKOs nie kleiner werden als ESR. Für die Eignung eines ELKOS, bei hohen Frequenzen Schaltreglerausgangsspannungen zu filtern, ist der ESR also von entscheidender Bedeutung. Bei 100kHz filtert ein 100µF-ELKO mit einem ESR von 24 Milliohm genausogut, wie ein 1000µF-ELKO mit einem ESR von 38 Milliohm. Beide haben einen Gesamtwechselstromwiderstand von ca. 40 Milliohm (ESR + Impedanz).

Leider liefern die üblichen 'Bastlerquellen' keine Angaben über den ESR der verkauften ELKOs. Man kann nur versuchen die Datenblätter der Kondensatorhersteller zu finden, oder man misst den ESR selbst.

Messung des ESR
Entweder man verwendet ein geeignetes ESR-Messgerät, ioder man misst "zu Fuß". Kleine ESR (im Milliohmbereich) werden nach der Konstantstrom-Methode gemessen. Dabei wird ein konstanter Wechselstrom mit konstanter Frequenz (üblicherweise 100 kHz) durch den ELKO geleitet. Der Spannungsabfall über dem ELKO resultiert aus ESR und Impedanz. Da die Impedanz aus Frequenz und Kapazität errechnet werden kann, lässt sich nun auch der ESR ermitteln. Oberhalb von 400µF kann man dabei die Impedanz  vernachlässigen.
 

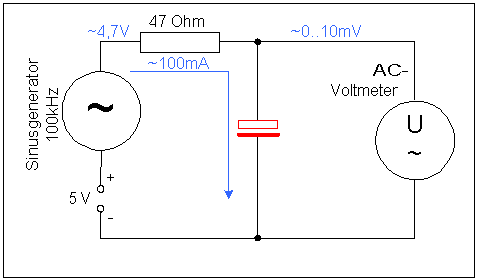Einen konstanten AC-Strom erhält man, indem man eine konstante AC-Spannung (z.B. 4,7 V) mit einem festen Widerstand abschließt.  Als Abschlusswiderstand dient bei mir die Reihenschaltung eines 47-Ohm-Widerstandes mit dem zu untersuchenden ELKO. Da die Summe aus ESR und Impedanz des ELKOs bei 100kHz unter 1 Ohm liegen sollte, kann sie für die Stromberechnung vernachlässigt werden. Der AC-Strom wird etwa 100mA betragen. Die zusätzliche 5V-Gleichspannung hält den Kondensator in einem geladenen Zustand, wie es ja im Normalbetrieb auch der Fall ist. (Je nach DC-Spannungsquelle kann es nötig sein, die Spannungsquelle mit einem großvolumigen ELKO zu überbrücken.) Das Voltmeter misst nun den AC-Spannungsabfall am Gesamtwechselstromwiderstand des ELKOs. Dabei entspricht 1 mV einem Widerstand von 10 Milliohm. Vom so ermittelten Gesamtwechselstromwiderstand wird die Impedanz abgezogen. Der verbleibende Betrag ist der ESR des ELKOs.

ACHTUNG:
Bitte ein AC-Voltmeter verwenden, das bei 100kHz noch funktioniert, oder anstelle des Voltmeters einen Oszi verwenden. Die meisten Standard-Multimeter messen nur bis 1kHz korrekt, und bei 100kHz gar nicht mehr.

Beispiel:
Wird in obriger Schaltung an einem 220µF-ELKO eine Wechselspannung con 3,5 mV gemessen, so beträgt der Gesamtwechselstromwiderstand 35 Milliohm. Abzüglich von 7,2 Milliohm Impedanz, verbleibt ein ESR von ca. 28 Milliohm.

Beispiele:

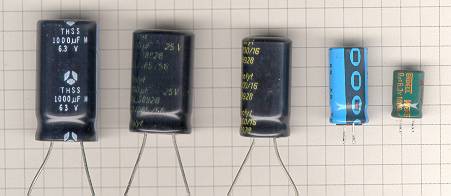Auf nebenstehendem Foto sind verschiedene 1000µF-Kondensatoren zu sehen, deren ESR ich ausgemessen habe. Von links nach rechts: 1000µF/63V, THSS, 44mOhm 1000µF/25V, Frolyt, 36mOhm 1000µF/16V, Frolyth, 42mOhm 1000µF/16V, Philips, 55mOhm 1000µF/6,3V,Wendell, 90mOhm

Sicherlich stellt jeder Hersteller auch andere Serien mit anderen Eigenschaften her, aber es fällt doch auf, dass der ESR von der mechanischen Größe des ELKOs abhängt. Die beiden Frolyt-Kondensatoren stammen noch aus DDR-Zeiten, und nicht aus der aktuellen Produktion. Da sie aber etwas größere Gehäuse besitzen als aktuelle Typen, weisen sie einen relativ kleinen ESR auf.
 

Auf nebenstehendem Foto sind zwei 220µF- und ein 2200µF-Kondensator zu sehen, deren ESR ich ausgemessen habe. Von links nach rechts: 220µF/25V, ????, 330mOhm 220µF/80V, Frolyt, 26mOhm   2200µF/63V,Samwha, 49mOhm

Der 220µF/80V-ELKO von Frolyt befindet sich im gleichen Gehäuse wie der 1000µF/25V-ELKO der gleichen Firma. Der ESR ist ähnlich klein. Der deutlich kleinere 220µF/25V-Typ disqualifiziert sich dagegen für Schaltreglerausgangssiebung durch seinen hohen ESR.
Interessant ist, dass der 2200µF-ELKO einen etwa doppelt so großen ESR hat wie der 220µF/80V-Typ. Bei 100 kHz filtert dieser 220µF/80V-ELKO deutlich besser als der 2200µF-Typ!!

Interessant ist auch ein Blick in Datenblätter der Hersteller. Frolyt gibt z.B. für seine EKR-Serie (ELKOs zur Nutzung in Schaltnetzteilen bei 10kHz...100kHz, Datenblatt vom Oktober 1997) maximale Gesamtwiderstände bei 100 kHz an. Für ELKOs im Gehäuse mit 12,5 mm Durchmesser und 21 mm Bauhöhe betragen der Gesamtwiderstand und der daraus folgende ESR:
 

Kapazität	1000µF	470µF	680µF	470µF	220µF	100µF
Spannung	10V	16V	16V	25V	40V	63V
Angegebener Rges.	90 mOhm	130 mOhm	100 mOhm	90 mOhm	130 mOhm	200 mOhm
errechnete Impedanz	1,6 mOhm	3,4 mOhm	2,3 mOhm	3,4 mOhm	7 mOhm	16 mOhm
ESR	88 mOhm	126 mOhm	98 mOhm	87 mOhm	123 mOhm	184 mOhm

All diese ELKOs sind mechanisch gleich groß, und haben etwa gleiche ESR, obwohl ihre Kapazität sehr verschieden ist.

Für ELKOSs  ab 220 µF hängt der Gesamtwiderstand bei Frequenzen oberhalb von 10 kHz nicht mehr von der Kapazität, sondern von der mechanischen Bauform (und damit vom ESR) ab. Eine bessere Siebung lässt sich dann nicht mehr durch eine einfache Vergrößerung der Kapazität erreichen, sondern durch die Wahl von ELKOS mit kleinem ESR (und großem Gehäuse) sowie durch das Parallelschalten von ELKOS.

Anstelle eines 1000-µF-ELKOS mit 88 mOhm sollte man z.B. lieber 5 Stück 220µF/80V ELKOS mit je 26 mOhm ESR einsetzen. Gemeinsam bilden diese eine Kapazität von 1100 µF bei 5 mOhm ESR, und unterdrücken das Sägezahnsignal eines Schaltreglers etwa 17 mal besser als der Einzel-ELKO.

Tantal-Elkos haben geringere ESR-Werte, allerdings werden sie auch nur für vergleichsweise kleine Kapazitäten hergestellt. Einen 22µF-Tantal-ELKO habe ich mit 80mOhm ESR ausgemessen. Im Vergleich mit einem normalen 22µF-ELKO kleiner Bauform ist das ein hervorragender Wert, aber mit 22 µF kann man nun mal nicht viel anfangen.

Fazit
Offensichtlich muss man bei Standard-ELKOS immer einen ESR von mindestens 50 mOhm erwarten, egal wie groß das Gehäuse oder die Kapazität ist. Kleinere ESR-Werte sind eher Glückssache. ELKOs mit kleinem Gehäuse und/oder kleiner Kapazität haben einen wesentlich größeren ESR. Zur groben Abschätzung verwende ich folgende empirische Näherungsformel:

• ESR [Ohm] = 50 000 / (C * V)

C: Kapazität in µF
V: Gehäusevolumen in cmm

• ESR [Ohm] = 60 000 / (C * h * d²)

C: Kapazität in µF
h: Gehäusehöhe in mm
d: Gehäusedurchmesser in mm

++HINWEIS++
Es gab den berechtigten Hinweis, das der ESR ein realer Widerdstand ist, während die Impedanz ein imaginärer Widerstand ist. Der Gesamtwiderstand, der sich aus beiden Werten zusammensetzt, ist nicht deren Summe, sondern die Wurzel der Summe ihrer Quadrate (hallo Pythagoras). Das hatte ich glatt übersehen, wodurch einige Berechnungen in diesem Abschnitt ungenau sind. Die Fehler sind aber nur bedeutend, wenn ESR und Impedanz in etwa ähnliche Werte haben. Sind sie aber sehr unterschiedlich (was meist der Fall ist) ist der Rechenfehler zu vernachlässigen.